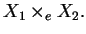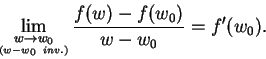Preliminaries

Here, we introduce some of the basic results of the theory of bicomplex numbers. First, we define bicomplex numbers as follows: $\mathbb {C}_{2}:=\{ a+bi_{1}+ci_{2}+dj:{i_1}^2={i_2}^2=-1, j^2=1\mbox{ and }i_2j=ji_2=-i_1,i_1j=ji_1=-i_2,i_2i_1=i_1i_2=j\}$ where $a,b,c,d\in\mathbb {R}$. The norm used on $\mathbb {C}_{2}$ is the Euclidean norm (also noted $\mid\mbox{ }\mid$) of $\mathbb {R}^{4}$. We remark that we can write a bicomplex number $a+bi_1+ci_2+dj$ as $(a+bi_1)+(c+di_1)i_2=z_1+z_2i_2$ where $z_1,z_2\in\mathbb {C}_{1}:=\{x+yi_1:{i_1}^{2}=-1\}$. Thus, $\mathbb {C}_{2}$ can be veiwed as the complexification of $\mathbb {C}_{1}$ and a bicomplex number can be seen as an element of $\mathbb {C}^{2}$. It is easy to see [13] that $\mathbb {C}_{2}$ is a commutative unitary ring with the following characterization for the noninvertible elements:

Proposition 1   Let $w=a+bi_1+ci_2+dj\in\mathbb {C}_{2}$. Then $w$ is noninvertible iff $(a=-d$ and $b=c)$ or $(a=d$ and $b=-c)$ iff ${z_1}^2+{z_2}^2=0$.

It is also possible to define differentiability of a function at a point of $\mathbb {C}_{2}$ [13]:

Definition 2   Let $U$ be an open set of $\mathbb {C}_{2}$ and $w_0\in U$. Then, $f:U\subseteq\mathbb {C}_{2}\longrightarrow\mathbb {C}_{2}$ is said to be $\mathbb {C}_{2}$-differentiable at $w_{0}$ with derivative equal to $f^\prime(w_0)\in\mathbb {C}_{2}$ if

$$\lim_{\stackrel{\scriptstyle w \rightarrow w_{0}} {\scriptsc... ...0}\mbox{ }inv.)}}\frac{f(w)-f(w_{0})}{w-w_{0}} =f^\prime(w_0).$$

We will also say that the function $f$ is $\mathbb {C}_{2}$-holomorphic on an open set U iff $f$ is $\mathbb {C}_{2}$-differentiable at each point of U.

As we saw, a bicomplex number can be seen as an element of $\mathbb {C}^{2}$, so a function $f(z_1+z_2i_2)=f_1(z_1,z_2)+f_2(z_1,z_2)i_2$ of $\mathbb {C}_{2}$ can be see as a mapping $f(z_1,z_2)=(f_1(z_1,z_2),f_2(z_1,z_2))$ of $\mathbb {C}^{2}$. Here we have a characterization of such mappings:

Theorem 3   Let U be an open set and $f:U\subseteq\mathbb {C}_{2}\longrightarrow\mathbb {C}_{2}$ such that $f\in {C}^{1}(U)$. Let also $f(z_1+z_2i_2)=f_1(z_1,z_2)+f_2(z_1,z_2)i_2$. Then $f$ is $\mathbb {C}_{2}$-holomorphic on U iff:

$$\mbox{$f_1$ and $f_2$ are holomorphic in $z_1$ and $z_2$}$$

and,

$$\frac{\partial{f_1}}{\partial{z_1}} =\frac{\partial{f_2}}{\p... ...rtial{z_1}} =-\frac{\partial{f_1}}{\partial{z_2}}\mbox{ on U}.$$

Moreover, $f^\prime=\frac{\partial{f_1}}{\partial{z_1}} +\frac{\partial{f_2}}{\partial{z_1}}i_2$ and $f^\prime(w)$ is invertible iff $det\mathcal{J}_{f}(w)\neq 0$.

This theorem can be obtained from results in [13] and [14]. Moreover, by the Hartogs theorem [19], it is possible to show that ``$f\in C^{1}(U)$" can be dropped from the hypotheses. Now, it is natural to define for $\mathbb {C}^{2}$ the following class of mappings introduced in [14]:

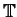
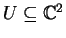
Definition 3   The class of $\mathbb {T}$-holomorphic mappings on a open set $U\subseteq\mathbb {C}^{2}$ is defined as follows:

$$\mbox{$TH(U):=$}\{f\mbox{:$U$}\subseteq\mathbb {C}^{2}\long... ...1}}=- \frac{\partial{f}_1}{\partial{z}_{2}}\mbox{ on $U$}\}.$$

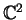
It is the subclass of holomorphic mappings of $\mathbb {C}^{2}$ satisfying the complexified Cauchy-Riemann equations.

In [14], bicomplex numbers were called tetranumbers and $\mathbb {C}_{2}$ was denoted by $\mathbb {T}$. In this article, we will use this notation when a definition can be written independently of the theory of bicomplex numbers . We remark that $f\in TH(U)$ iff $f$ is $\mathbb {C}_{2}$-holomorphic on U. It is also important to know that every bicomplex number $z_1+z_2i_2$ has the following unique idempotent representation:

$$z_1+z_2i_2=(z_1-z_2i_1)e_1+(z_1+z_2i_1)e_2$$

where $e_1=\frac{1+j}{2}$ and $e_2=\frac{1-j}{2}$. This representation is very useful because: addition, multiplication and division can be done term-by-term. Also, an element will be noninvertible iff $z_1-z_2i_1=0$ or $z_1+z_2i_1=0$. The notion of holomorphicity can also be see with this kind of notation. For this we need to define the functions $h_1,h_2:\mathbb {C}_{2}\longrightarrow\mathbb {C}_{1}$ as $h_1(z_1+z_2i_2)=z_1-z_2i_1$ and $h_2(z_1+z_2i_2)=z_1+z_2i_1$. Also, we need the following definition:

Definition 4   We say that $X\subseteq\mathbb {C}_{2}$ is a $\mathbb {C}_{2}$-cartesian set determined by $X_1$ and $X_2$ if $X=X_{1}\times_e X_{2}:=\{z_1+z_2i_2\in\mathbb {C}_{2}:z_1+z_2i_2=w_1e_1+w_2e_2, (w_1,w_2)\in X_1\times X_2\}$.

In [13] it is shown that if $X_1$ and $X_2$ are domains of $\mathbb {C}_{1}$ then $X_1\times_e X_2$ is also a domain of $\mathbb {C}_{2}$. Now, it is possible to state the following striking theorems [13]:

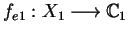
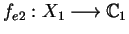
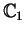
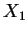
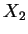
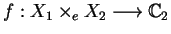
Theorem 4   If $f_{e1}:X_1\longrightarrow \mathbb {C}_{1}$ and $f_{e2}:X_1\longrightarrow \mathbb {C}_{1}$ are holomorphic functions of $\mathbb {C}_{1}$ on the domains $X_1$ and $X_2$ respectively, then the function $f:X_1\times_e X_2\longrightarrow \mathbb {C}_{2}$ defined as

$$f(z_1+z_2i_2)=f_{e1}(z_1-z_2i_1)e_1+f_{e2}(z_1+z_2i_1)e_2,\mbox{ }\forall\mbox{ }z_1+z_2i_2\in X_1\times_e X_2$$

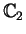
is $\mathbb {C}_{2}$-holomorphic on the domain $X_1\times_e X_2.$

Theorem 5   Let $X$ be a domain in $\mathbb {C}_{2}$, and let $f:X\longrightarrow\mathbb {C}_{2}$ be a $\mathbb {C}_{2}$-holomorphic function on X. Then there exist holomorphic functions $f_{e1}:X_1\longrightarrow \mathbb {C}_{1}$ and $f_{e2}:X_2\longrightarrow\mathbb {C}_{1}$ with $X_1=h_1(X)$ and $X_2=h_2(X)$, such that:

$$f(z_1+z_2i_2)=f_{e1}(z_1-z_2i_1)e_1+f_{e2}(z_1+z_2i_1)e_2,\mbox{ }\forall \mbox{ }z_1+z_2i_2\in X.$$

We note here that $X_1$ and $X_2$ will also be domains of $\mathbb {C}_{1}$.

Finally we give some concrete simple examples of entire $\mathbb {T}$-holomorphic mappings which come from the bicomplex theory. First, the exponential mapping defined as:

$$e^{z_1+z_2i_2}:=e^{z_1}(cos(z_2)+i_2sin(z_2))=e^{z_1-z_2i_1}e_1+e^{z_1+z_2i_2}e_2,$$

with $e^{w_1+w_2}=e^{w_1}\cdot e^{w_2},\mbox{ }\forall\mbox{ } w_1,w_2\in\mathbb {C}_{2}$ and $(e^{w})^\prime =e^{w},\mbox{ }\forall\mbox{ } w\in\mathbb {C}_{2}$. Secondly, the polynomials of degree n, with bicomplex multiplication, defined as:

$${a}_{1}\cdot{w}^{n} + {a}_{2}\cdot{w}^{n-1}+...+{a}_{n},$$

with $a_i\in\mathbb {C}_{2}$ for $i=1,...,n$ and $w\in\mathbb {C}_{2}$. We note that the derivative will be what we expect for polynomials.